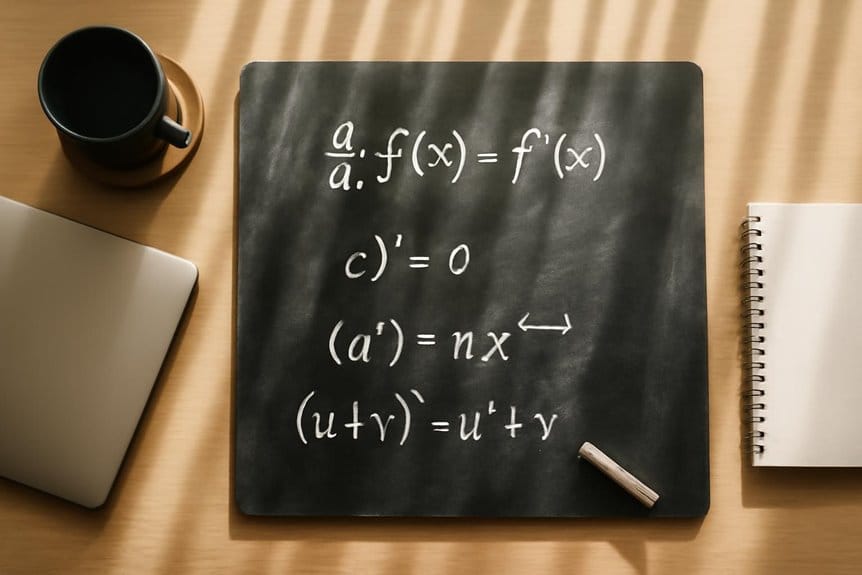A thorough guide to differentiation rules is essential for understanding calculus. It covers foundational rules like the Power Rule, constant multiple rule, and sum/difference rule. Advanced sections detail the Product, Quotient, and Chain Rules, critical for complex functions. Derivatives of trigonometric, exponential, and logarithmic functions are explained. The guide also explores differentiating implicit functions. Each rule is fundamental for analyzing rates of change across various disciplines. Explore further to solidify your grasp on these crucial concepts.

Key Takeaways

• Learn fundamental rules like the power rule for differentiating x^n.
• Master basic rules: constant multiple, sum, difference, product, and quotient.
• Understand derivatives of special functions like exponential, logarithmic, and trigonometric.
• Differentiate implicit functions by treating y as a function of x.
• Utilize technology and practice for mastering differentiation rules.

The Power Rule Made Clear

When faced with differentiating a function of the form $f(x) = x^n$, where $n$ is any real number, the power rule provides a straightforward method. This fundamental rule dictates that the derivative of $x^n$ is $nx^{n-1}$. The power rule application is vital for simplifying many calculus problems. For instance, the derivative of $x^3$ is found by bringing the exponent 3 down as a coefficient and reducing the exponent by one, resulting in $3x^2$. Similarly, for a function like $f(x) = x^{1/2}$, its derivative is $(1/2)x^{-1/2}$, showcasing its versatility. These derivation examples illustrate the direct translation of the rule into practice. Understanding the power rule is the bedrock for performing more complex differentiation using other calculus rules. HyperWrite’s AI writer can assist in generating detailed explanations and examples of such calculus concepts, enhancing learning and comprehension.

Mastering the Constant Multiple Rule

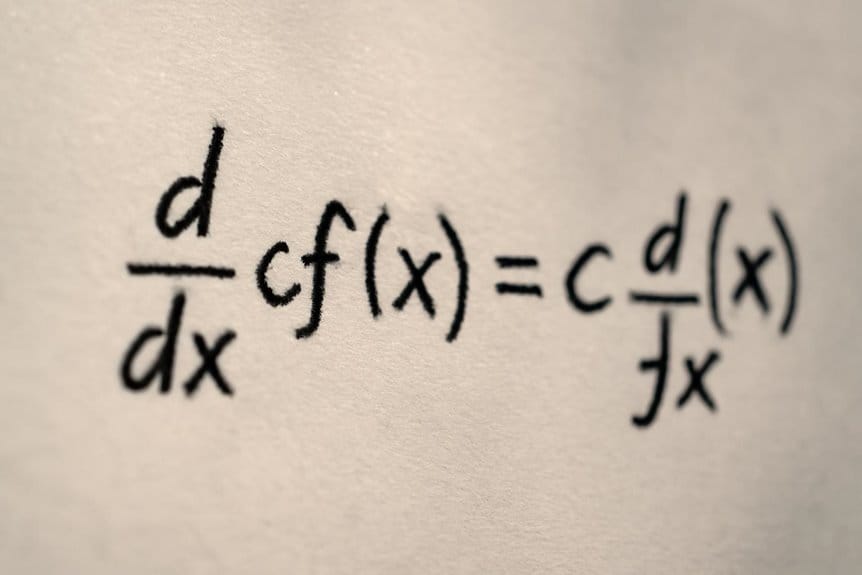
Building on the foundation established by the power rule, the constant multiple rule addresses how to differentiate functions involving a constant multiplied by a variable expression. This rule states that the derivative of a constant times a function is equal to the constant times the derivative of the function.

Mathematically, if $c$ is a constant and $f(x)$ is a differentiable function, then $rac{d}{dx}[c cdot f(x)] = c cdot rac{d}{dx}[f(x)]$.

This principle is fundamental because it allows for the simplification of differentiation processes. When encountering constant multiples within a function, the procedure is to extract these scalar factors and proceed with differentiating the remaining variable expression. This ease of use is reminiscent of the clean and intuitive layout found in certain AI writing tools, which prioritize simplicity for users.

This approach streamlines calculations, making the differentiation of more complex functions readily manageable by isolating the effect of the constant multiplier.

Sum and Difference Rule Demystified

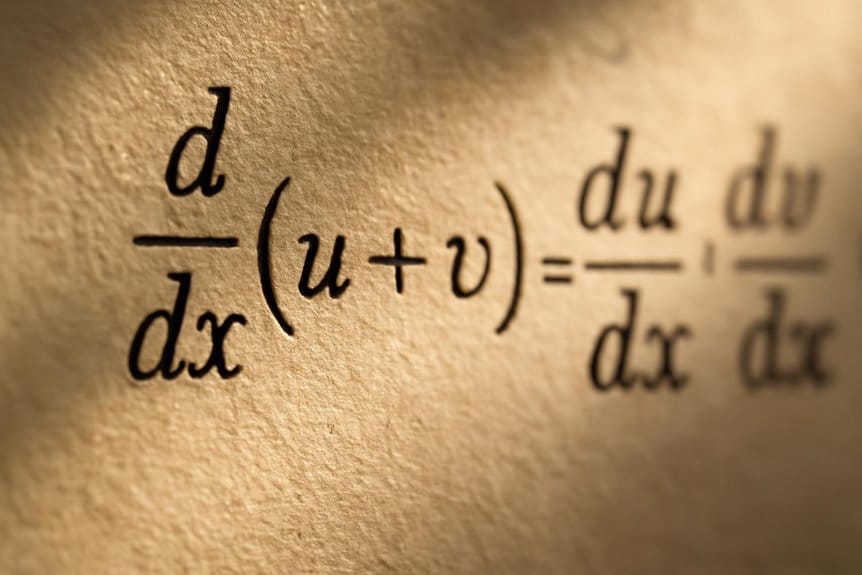
The sum and difference rule provides a straightforward method for differentiating functions that are sums or differences of simpler expressions. This fundamental rule states that the derivative of a sum of functions is the sum of their derivatives, and similarly, the derivative of a difference is the difference of their derivatives. For instance, if (f(x) = g(x) + h(x)), then (f'(x) = g'(x) + h'(x)). This principle extends naturally to any finite number of terms. Understanding this rule is essential for handling more complex derivatives, including those involving chain rule applications. Numerous sum rule examples illustrate its utility, such as differentiating polynomials. This rule simplifies the process of differentiation greatly by breaking down complex functions into manageable components. To enhance your understanding of differentiation, exploring creative flexibility in writing tools like Sudowrite can aid in visualizing complex mathematical concepts and improve your problem-solving skills.

Harnessing the Product Rule

Why might one need a rule beyond the sum and difference? Certain functions in calculus arise from the multiplication of two or more simpler functions. The product rule provides a systematic method for differentiating such composite functions.

This rule states that the derivative of a product of two functions, $f(x)$ and $g(x)$, is $(fg)’ = f’g + fg’$.

Key aspects of the product rule include:

• Understanding the structure of functions that are products of terms.
• Applying the rule correctly to various product rule examples.
• Recognizing product rule applications in fields like physics and economics.
• Differentiating chained products using iterative application of the rule.
• Just as Grammarly provides real-time writing assistance, implementing the product rule offers real-time clarity to calculus problems involving product functions.

Tackling the Quotient Rule

While the product rule addresses functions formed by multiplication, some expressions in calculus are formed by division. The quotient rule provides a systematic method for differentiating such functions, often denoted as $f(x) = frac{g(x)}{h(x)}$.

The formula for the quotient rule is:

$$f'(x) = frac{g'(x)h(x) – g(x)h'(x)}{[h(x)]^2}$$

This rule is fundamental in various calculus problems and has broad quotient rule applications in fields like physics and engineering where rates of change of quotients are common. Understanding and correctly applying the quotient rule is essential. To further enhance comprehension, it is beneficial to focus on well-researched examples and practice problems that illustrate the rule in real-world scenarios.

However, common quotient rule pitfalls include misremembering the order of terms in the numerator or incorrectly squaring the denominator. Careful attention to the formula’s structure mitigates these errors.

The Versatile Chain Rule Explained

How does one differentiate composite functions, those built by nesting one function inside another, such as $f(x) = (2x^3 – 1)^4$? The answer lies in the chain rule, a fundamental concept for calculating composite function derivatives.

This rule states that the derivative of a composite function $f(g(x))$ is the derivative of the outer function evaluated at the inner function, multiplied by the derivative of the inner function.

Key aspects of the chain rule include:

1. Understanding Composition: Recognizing when a function is composed of two or more simpler functions.
2. Identifying Outer and Inner Functions: Clearly distinguishing the “outer” and “inner” components of the composite function.
3. Applying the Rule Iteratively: For functions nested more than twice, applying the rule sequentially.
4. Chain Rule Applications: Its broad utility in various calculus problems, including implicit differentiation and related rates, solidifies its importance.

Incorporating AI tools in modern writing can aid in overcoming challenges like writer’s block by automating routine tasks, enhancing productivity, and providing fresh perspectives.

Derivatives of Trigonometric Functions

Calculus offers specific rules for differentiating trigonometric functions, which are fundamental to many areas of mathematics and science. The derivatives of these functions, such as sine and cosine, are derived using the limit definition and are closely related to the geometry of the unit circle.

The foundational derivative is $(sin x)’ = cos x$, and $(cos x)’ = -sin x$.

Other trigonometric functions, including tangent, cotangent, secant, and cosecant, have derivatives that can be found by applying the quotient rule or product rule to sine and cosine, or by considering their definitions in terms of sine and cosine.

For instance, the derivative of $tan x$ is $sec^2 x$. The derivatives of the reciprocal functions follow the same principles.

Significantly, $(sec x)’ = sec x tan x$ and $(csc x)’ = -csc x cot x$.

Understanding these relationships, often visualized on the unit circle, is essential for solving a wide range of problems in fields like physics and engineering. Using AI tools, such as Sudowrite for brainstorming, can enhance the process of learning and applying these differentiation rules by providing engaging and personalized content.

Exponential and Logarithmic Derivatives

When exploring the landscape of calculus, attention often turns to the derivatives of exponential and logarithmic functions, essential tools for modeling growth and decay.

The derivative of the natural exponential function, $e^x$, is simply $e^x$ itself. For a general exponential function $a^x$, its derivative is $a^x ln(a)$. The derivative of the natural logarithm, $ln(x)$$, is $1/x$.

Key rules for these functions include:

1. Derivative of $e^{u(x)}$ is $e^{u(x)} cdot u'(x)$.
2. Derivative of $a^{u(x)}$ is $a^{u(x)} ln(a) cdot u'(x)$.
3. Derivative of $ln(u(x))$ is $rac{1}{u(x)} cdot u'(x)$.
4. Logarithmic differentiation is a technique used when dealing with complex exponential functions.

In modern content creation, AI writing assistants are revolutionizing how educational material on complex topics like calculus is generated, ensuring accuracy and coherence with minimal human intervention.

Differentiating Implicit Functions

The process involves treating *y* as a function of *x* and applying the chain rule. Differentiating implicit equations term by term with respect to *x*, remembering that the derivative of *y* with respect to *x* is *dy/dx*. After differentiating all terms, the next step is to algebraically rearrange the resulting equation to solve for *dy/dx*. This analytical approach allows for the calculation of instantaneous rates of change within these complex relationships. By utilizing AI technologies, content creators can automate content generation for various formats, enhancing productivity and innovation in the field.